这是定积分原理推导的第二道题目，先看英文原题：

show that$${\int }_1^b{\displaystyle \frac{1}{x^2}}dx=1-{\displaystyle \frac{1}{b}}$$by using equal subintervals and taking $x_k^{\ast }=\sqrt{x_{k-1}\cdot x_k}$ in formula (12) of Section 6.4（同第一题中所指公式）。

还是一样，先画出草图

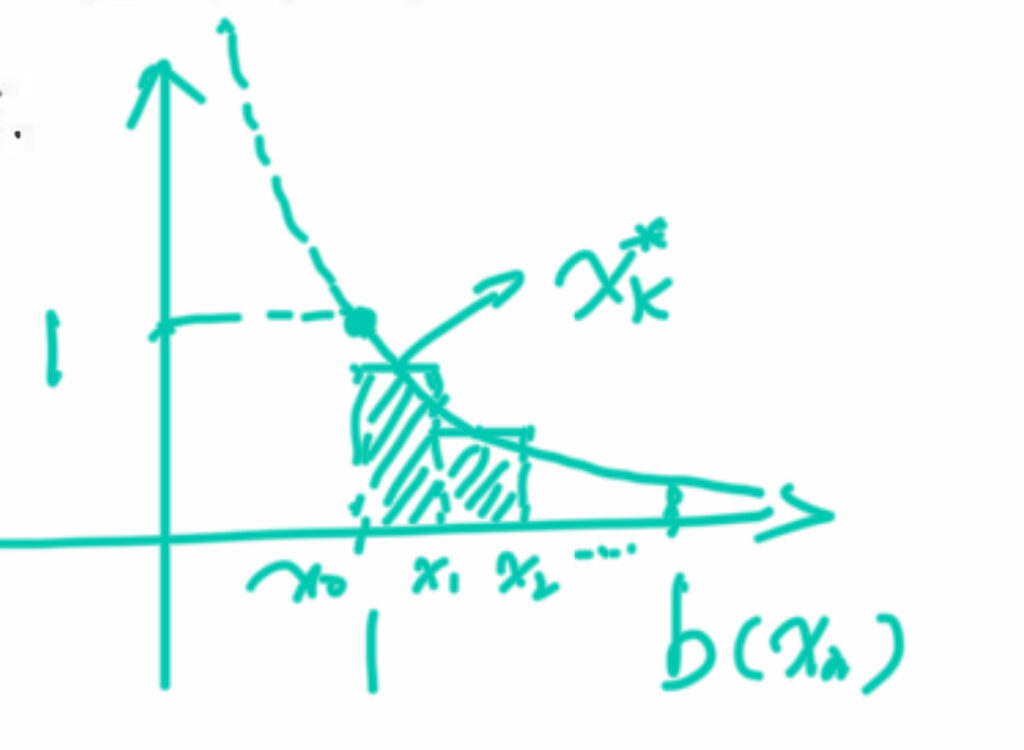
首先，根据定积分的定义以及题意，可知将1和b之间分成n等份，由此将该曲线与x轴之间的面积分成n个长方形。

得到每个长方形的底边（也就是每等份之间隔）为${\displaystyle \frac{b-1}{n}}$，为了方便起见，我们将${\displaystyle \frac{b-1}{n}}$记为$m$

再用 $m$ 分别表示$x_0$、$x_1$、$x_n$等

$$\begin{array}{rl}{x}_0& =1\\ x_1& =1+m\\ x_2& =1+2m\\ ⋮\\ x_n& =1+nm=b\end{array}$$

再根据题目之要求，taking $x_k^{\ast }=\sqrt{x_{k-1}\cdot x_k}$ in formula (12) of Section 6.4，得到

$$\begin{array}{rl}{x}_1^{\ast }& =\sqrt{x_0\cdot x_1}=\sqrt{1\cdot (1+m)}\\ x_2^{\ast }& =\sqrt{x\cdot x_2}=\sqrt{(1+m)\cdot (1+2m)}\\ ⋮\\ x_n^{\ast }& =\sqrt{x_{n-1}\cdot x_n}=\sqrt{[1+(n-1)m]\cdot (1+nm)}\end{array}$$

再根据$f\left(x\right)={\displaystyle \frac{1}{x^2}}$,得到每个长方形的高：

$$\begin{array}{rl}f\left(x_1^{\ast }\right)& ={\displaystyle \frac{1}{1\cdot (1+m)}}\\ f\left(x_2^{\ast }\right)& ={\displaystyle \frac{1}{(1+m)\cdot (1+2m)}}\\ ⋮\\ f\left(x_n^{\ast }\right)& ={\displaystyle \frac{1}{[1+(n-1)m]\cdot (1+nm)}}\end{array}$$

再计算得到每个长方形之面积如下：

$$\begin{array}{rl}{S}_1& =f\left(x_1^{\ast }\right)\cdot m={\displaystyle \frac{1}{1\cdot (1+m)}}\cdot m\\ S_2& =f\left(x_2^{\ast }\right)\cdot m={\displaystyle \frac{1}{(1+m)\cdot (1+2m)}}\cdot m\\ ⋮\\ S_n& =f\left(x_n^{\ast }\right)\cdot m={\displaystyle \frac{1}{[1+(n-1)m]\cdot (1+nm)}}\cdot m\end{array}$$

原题中还有一个提示，可以直接帮助解决这个求和问题：

Hint: It will be necessary to use a variation of the idea behind the formula$$\begin{array}{rl}{\displaystyle \frac{1}{1\cdot 2}}+{\displaystyle \frac{1}{2\cdot 3}}+\dots +{\displaystyle \frac{1}{(n-1)n}}& ={\displaystyle \frac{1}{1}}-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{3}}+\dots -{\displaystyle \frac{1}{n}}\\ & =1-{\displaystyle \frac{1}{n}}\end{array}$$

在此，稍加注意：$$\begin{array}{rl}{\displaystyle \frac{1}{1}}-{\displaystyle \frac{1}{1+m}}& ={\displaystyle \frac{1+m-1}{1\cdot (1+m)}}\\ & ={\displaystyle \frac{m}{1\cdot (1+m)}}\end{array}$$

从而很容易得出所有长方形的面积之和为：$$\begin{array}{rl}{S}_{sum}& =S_1+S_2+\dots +S_n\\ & ={\displaystyle \frac{1}{1}}-{\displaystyle \frac{1}{1+m}}+{\displaystyle \frac{1}{1+m}}-{\displaystyle \frac{1}{1+2m}}+\dots -{\displaystyle \frac{1}{1+nm}}\\ & =1-{\displaystyle \frac{1}{1+nm}}\end{array}$$

最后将上式中的 $m$ 替换为 ${\displaystyle \frac{b-1}{n}}$ 得到：

$$\begin{array}{rl}1-{\displaystyle \frac{1}{1+nm}}={\displaystyle \frac{nm}{1+nm}}& ={\displaystyle \frac{b-1}{b}}\\ & =1-{\displaystyle \frac{1}{b}}\end{array}$$

证毕