题目是自己翻译的,也不知道准不准确,反正大概意思就是这样,结合图片应该就没理解上的问题了。
下面是原题表述:
The shaded region inside the square of side $a$ shown in Fig. 7.6 consists of all points that are closer to the center of the square than to its boundary. Find the area of this region.
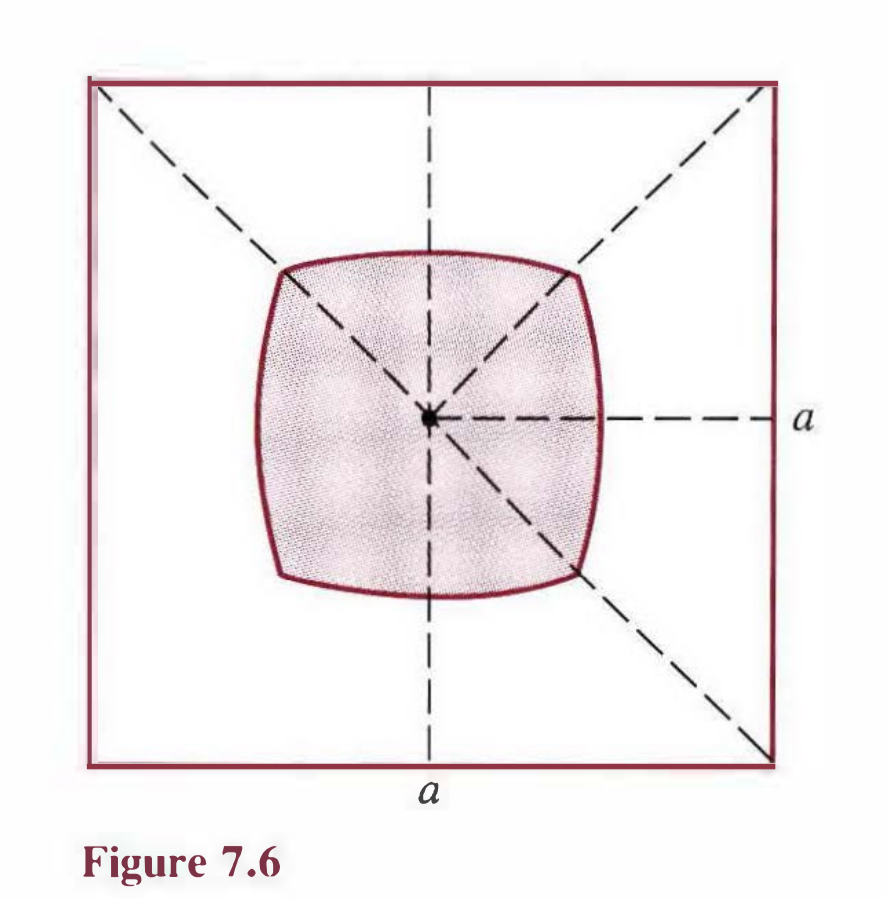
解决本题时,有两个错误比较容易出现(自身经历)
1、阴影中的点是在其两个距离之间进行比较,一个是与正方形中心的距离(这个不会有问题),一个是与正方形边的距离(这个容易出现问题,容易想成是与正方形顶点的距离,尤其是在对角线的情形下)
2、正方形边长为$a$,因此在建立的坐标系中,建立的方程应该是以$\dfrac{1}{2}a$为基础
下面开始进入解决步骤:
以正方形中心为原点建立坐标系,首先利用阴影图形的对称性,我们只需要计算出第一象限中上半部分的面积即可得出整体面积,乘以$8$即可。
而计算第一象限中上半部分的面积,我们需要知道阴影部分在这部分中边界曲线的方程,而这个方程可以由阴影部分中所有点均具备“all points that are closer to the center of the square than to its boundary”这一特性得到,当然我们还是只需要考虑阴影部分的边界即可(边界应该正好是两个距离相等的点的集合),除此之外,我们还需要注意一点:第一象限中上半部分的阴影内所有的点,与其距离最近的边都是上边。假如此时讨论边界上的点坐标为$\left( x,y\right)$,由此得到两个距离的表达式如下:
距离中心:$\sqrt{x^{2}+y^{2}}$
距离最近的边(上边):$\dfrac{1}{2}a-y$
根据定义可知:$$\begin{aligned}\sqrt{x^{2}+y^{2}}&=\dfrac{a}{2}-y\ \\
x^{2}+y^{2}&=\left( \dfrac{a}{2}-y\right) ^{2}\ \\
y&=-\dfrac{1}{a}x^{2}+\dfrac{1}{4}a\end{aligned}$$
由此,我们得到第一部分我们想要曲线的方程,我们再来计算这段曲线最右端的横坐标,显然,此时该曲线与$y=x$相交。可以得到以下方程:$$-\dfrac{1}{a}x^{2}+\dfrac{1}{4}a=x$$
解该方程得到:$$x=\dfrac{\sqrt{2}-1}{2}a$$
至此,我们已经得到我们所需要的所有必要的量来通过积分计算得到该曲线与x轴之间形成的面积,通过积分计算如下:
$$\begin{aligned}\int ^{\dfrac{\sqrt{2}-1}{2}a}_{0}\left( -\dfrac{1}{a}x^{2}+\dfrac{1}{4}a\right) dx\ &=\left( -\dfrac{x^{3}}{3a}+\dfrac{ax}{4}\right) ]_ {0}^{\dfrac{\sqrt{2}-1}{2}a}\ \\
&=\dfrac{2-\sqrt{2}}{12}a^{2}\end{aligned}$$
至此,最关键的一步,同时也是最容易出错的一步,通过积分计算的面积包含了一部分我们不需要的面积($y=x$与$x$轴之间形成的直角三角形),因此我们需要将该部分剔除,得到:
$$\begin{aligned}\dfrac{2-\sqrt{2}}{12}a^{2}-\dfrac{1}{2}\cdot \left( \dfrac{\sqrt{2}-1}{2}a\right) ^{2}\
=\dfrac{4\sqrt{2}-5}{24}a^{2}\end{aligned}$$
最后,将该部分乘以8,即得到我们最终的答案:
$$\begin{aligned}\dfrac{4\sqrt{2}-5}{24}a^{2}\times 8&=\dfrac{4\sqrt{2}-5}{3}a^{2}\ \\
&\approx 0.21895a^{2}\end{aligned}$$