我们设任意直线$ax+by+c=0$

然后设直线外任意一点的坐标为$\left( x_{0},y_{0}\right)$

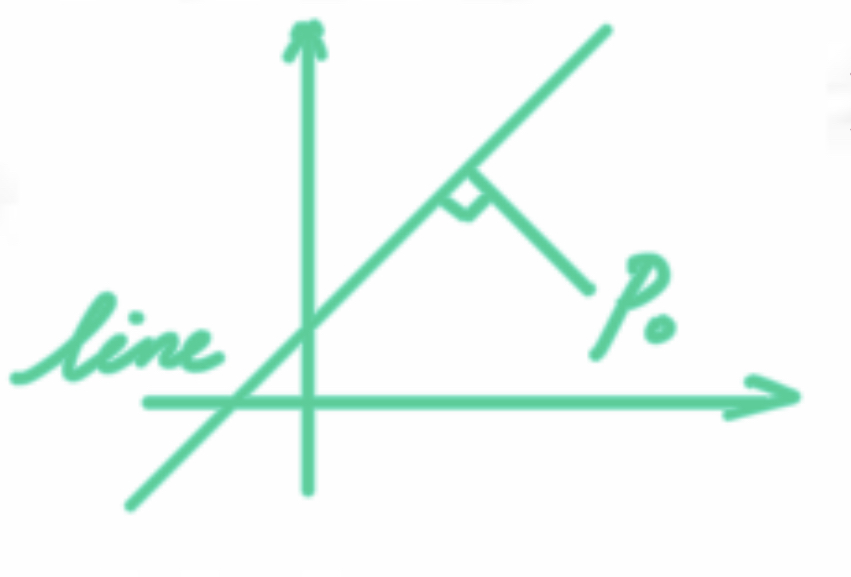
显然，该点到已知直线最短的距离，应当为过点$p_{0}$作已知直线的垂线（这个结论通过微积分可以很简单得到证明，在此不作赘述），设前述交点的坐标为$\left( x,y\right)$，又因为直线的斜率为$-\dfrac{a}{b}$，可以得到点$p_{0}$和交点确定的直线斜率为$\dfrac{b}{a}$，从而得到以下关键等式：$$\dfrac{y-y_{0}}{x-x_{0}}=\dfrac{b}{a}$$又设点到直线距离为S，则根据勾股定理，有：$$S^{2}=\left( y-y_{0}\right) ^{2}+\left( x-x_{0}\right) ^{2}$$将前面关键等式，替换到上面这个等式得到：$$\begin{aligned}S^{2}&=\dfrac{b^{2}}{a^{2}}\left( x-x_{0}\right) ^{2}+\left( x-x_{0}\right) ^{2}\ \\&=\dfrac{a^{2}+b^{2}}{a^{2}}\left( x-x_{0}\right) ^{2}\end{aligned}$$因此有：$$S=\dfrac{\sqrt{a^{2}+b^{2}}}{a}\cdot \left( x-x_{0}\right)$$又因为：$y=-\dfrac{a}{b}x-\dfrac{c}{b}$和$\dfrac{y-y_{0}}{x-x_{0}}=\dfrac{b}{a}$，可以得到下面等式：$$x-x_{0}=\dfrac{-a^{2}x-ac-aby_{0}}{b^{2}}$$将这个表达式替换到前面S的等式中，得到：$$\begin{aligned}S &=\dfrac{\sqrt{a^{2}+b^{2}}}{a}\cdot \left( \dfrac{-a^{2}x-ac-aby\cdot }{b^{2}}\right) \ \\&=\sqrt{a^{2}+b^{2}}\cdot \left( \dfrac{-ax-c-by_{0}}{b^{2}}\right) \end{aligned}$$再将直线方程和前面最开始的关键等式结合，得到：$$\begin{aligned}\dfrac{-\dfrac{a}{b}x-\dfrac{c}{b}-y_{0}}{x-x_{0}}=\dfrac{b}{a}\end{aligned}$$和$$\begin{aligned}x-x_{0}=-\dfrac{a^{2}}{b^{2}}x-\dfrac{ac}{b^{2}}-\dfrac{aby_{0}}{b^{2}}\end{aligned}$$我们的目的是用所有已知量表达未知量x，继续：$$\begin{aligned}\dfrac{a^{2}+b^{2}}{b^{2}}x&=-\dfrac{ac}{b^{2}}-\dfrac{aby_{0}}{b^{2}}+x_{0}\ \\&=\dfrac{-ac-aby_{0}+b^{2}x_{0}}{b^{2}}\end{aligned}$$最终得到：$$x=\dfrac{-ac-aby_{0}+b^{2}x_{0}}{a^{2}+b^{2}}$$将这个关于x的表达式替换到前面S的表达式中得到：$$\begin{aligned}S&=\sqrt{a^{2}+b^{2}}\cdot \dfrac{-ax-c-by_{0}}{b^{2}}\ \\&=\dfrac{\sqrt{a^{2}+b^{2}}}{b^{2}}\cdot \left( -ax-c-by_{0}\right) \
\\&=\dfrac{\sqrt{a^{2}+b^{2}}}{b^{2}}\cdot \dfrac{-a\left( -ac-aby_{0}+b^{2}x_{0}\right) -bc^{2}-a^{2}c-b^{3}y_{0}-a^{2}by_{0}}{a^{2}+b^{2}}\
\\&=\dfrac{1}{b^{2}}\cdot \dfrac{a^{2}c+a^{2}by_{0}-ab^{2}x_{0}-b^{2}c-a^{2}c-b^{3}y_{0}-a^{2}by_{0}}{\sqrt{a^{2}+b^{2}}}\
\\&=\dfrac{\left| ax_{0}+by_{0}+c\right| }{\sqrt{a^{2}+b^{2}}}\end{aligned}$$

推导完毕