首先,来看看这幅具有美感的函数图形。
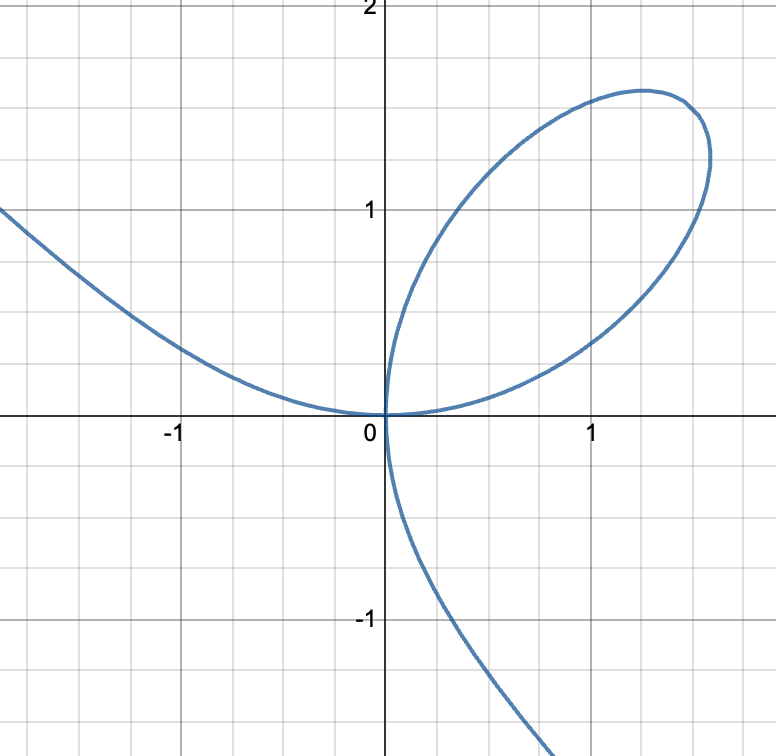
显然,从图中也可以大致看出最高点在于1.5到2之间。。。。。
我们先将$$x^{3}+y^{3}=3xy$$写成$$y^{3}=3xy-x^{3}$$然后同时运用链式法则和幂法则对等式两边进行微分,也就是求导,可以得到:$$3y^{2}\cdot \dfrac{dy}{dx}=3x\cdot \dfrac{dy}{dx}+3y-3x^{2}$$移项可得:$$\left( 3y^{2}-3x\right) \dfrac{dy}{dx}=3y-3x^{2}$$从而得到:$$\dfrac{dy}{dx}=\dfrac{3y-3x^{2}}{3y^{2}-3x}=\dfrac{y-x^{2}}{y^{2}-x}$$若要求函数的极值,则极值处该函数的导数应该为0,因此,令$\dfrac{dy}{dx}$为0,即:$$y-x^{2}=0$$即:$$y=x^{2}$$将上述等式代入$$x^{3}+y^{3}=3xy$$得到:$$x^{3}+x^{6}=3x^{3}$$令$$z=x^{3}$$则以上等式变为$$z+z^{2}=3z$$从而,可以解得$z=2$,也就是$x^{3}=2$,也就是在$x=\sqrt[3] {2}$时,该函数达到最大值$\sqrt[3] {4}$