A trough is to be made from three planks, each 12 in wide. If the cross section has the shape of a trapezoid, how far apart should the tops of the sides be placed to give the trough maximum carrying capacity?
说实话,看到这道题目,半天没懂个啥意思,搜了半天google,换了n种方式问chatgpt,都没找到自己想要的。说来也奇怪,在毫无头绪的时候,在毫无征兆的一瞬间又突然想通这个题目到底想要自己解决一个什么问题了。
好吧,出现上面这个和我一样问题的肯定也是英文跟我一样蹩脚的,立志需谨慎,毕竟我们是要做到有恒的,好吧,一切困难都会解决的,一切问题都只是暂时的。
进入正题,先说说题目说的啥,其实很简单,三块宽12英寸(单位无所谓,我们更需要关注数学本身,而不需要关注这些)的木板,长度任意,组合成一个横截面为梯形的水槽,既然是水槽,所以顶部是空的,所以三块木板即可完成。(一开始自己还想着乱七八糟的样子,锥形什么的)因为木板长度任意,所以我们只需要关注横截面的面积大小即可。
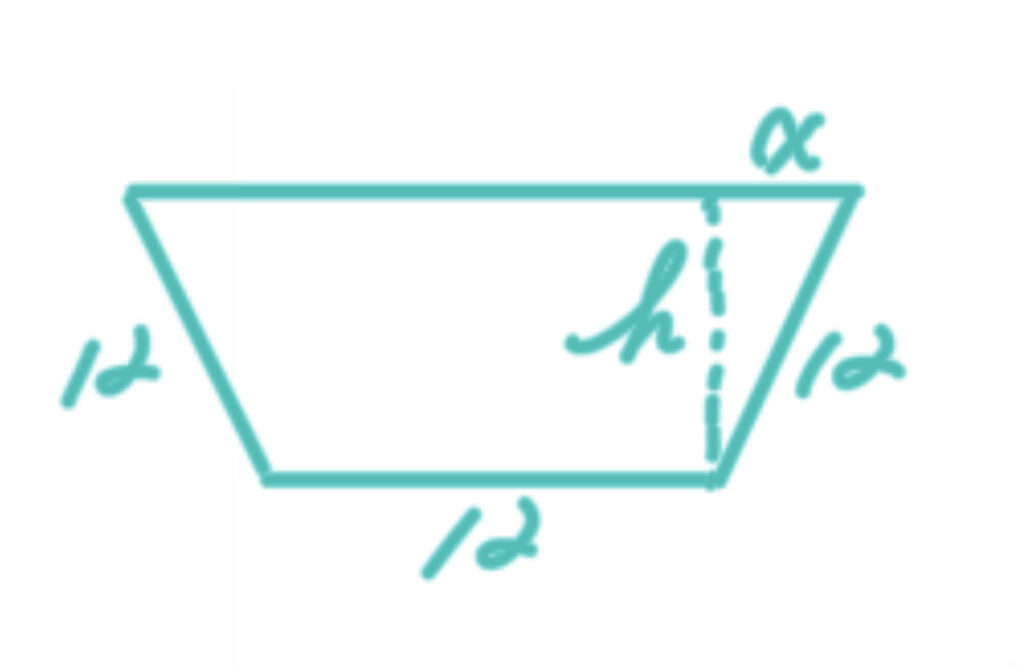
所以问题就转换为一句话:上图中两侧的木板分开多少角度?或者说两侧木板的顶部分开多远?这个梯形面积可以取到最大值。
如图所示,将梯形的高设为h,上边比下边长出x英寸(仅仅一边长出x),相信结合图片,应该不会有歧义。
根据勾股定理,我们可以得到
根据梯形的面积公式,可以得到梯形的面积表达式:
对上述面积方程进行微分,得到:
再重新回到前面的x^{2}+h^{2}=144,对其进行微分,得到:
从而得到:
将这个式子代入\dfrac{dA}{dx}得到:
又根据微分性质可得,当梯形面积最大时,\dfrac{dA}{dx}的值应当为0:
从而得到面积最大时,h和x的数量关系:
将这个数量关系再代入最前面由勾股定理得到的等式,即可解出答案:
因为x必然是正数,因此x为6英寸时,梯形面积取到最大值。