今天自己有点高产了，居然连着两篇文章。

还是先看原题：

然后还是草图：

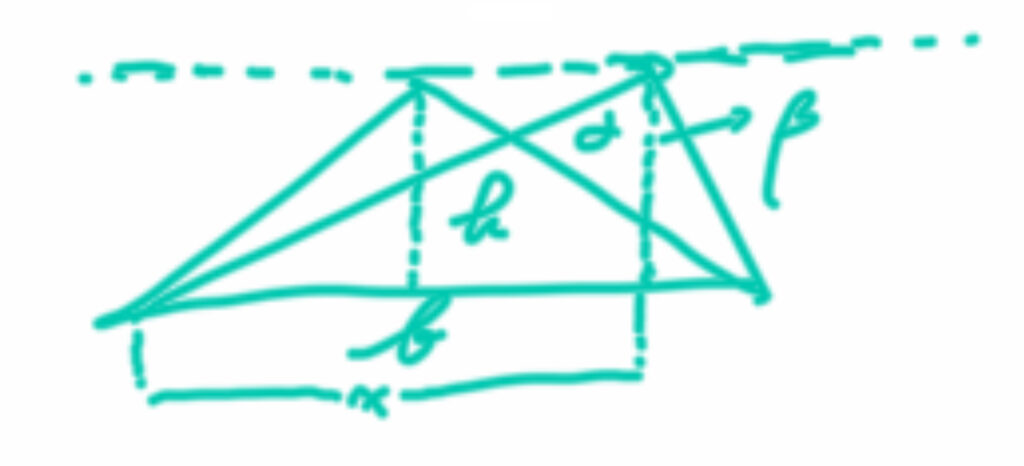
接着还是各个符号的具体意义：

三角形面积：$A$

三角形底边长：$b$

根据三角形面积公式，可以得出三角形的高此时是固定的：$$\begin{aligned}A&=\dfrac{1}{2}bh\ \\
h&=\dfrac{2A}{b}\end{aligned}$$

那么当该三角形的上顶点在上面这条直线中左右移动时，就会呈现一个动态的情形，会有无数个符合条件的三角形，我们需要证明当该三角形为等腰时，上顶角最大，即$\alpha +\beta$最大。

思路依然是建立$\alpha +\beta$的表达式，然后进行求导，令导数等于zero，此时便找到了我们想要的。那么开始吧！

根据三角形、三角函数以及反三角函数的性质，显然：

$$\begin{aligned}\tan \alpha &=\dfrac{x}{h}\ \\
&=\dfrac{x}{\dfrac{2A}{b}}=\dfrac{bx}{2A}\ \\
\alpha &=\tan ^{-1}\dfrac{bx}{2A}\end{aligned}$$

$$\begin{aligned}\tan \beta &=\dfrac{b-x}{h}\ \\
&=\dfrac{b-x}{\dfrac{2A}{b}}=\dfrac{b^{2}-bx}{2A}\ \\
\beta &=\tan ^{-1}\dfrac{b^{2}-bx}{2A}\end{aligned}$$

很简单的获取了$\alpha +\beta$关于$x$的表达式：

$$\begin{aligned}\alpha +\beta &=\tan ^{-1}\dfrac{bx}{2A}+\tan ^{-1}\dfrac{b^{2}-bx}{2A}\ \\
\dfrac{d\left( \alpha +\beta \right) }{dx}&=\dfrac{1}{1+\left( \dfrac{bx}{2A}\right) ^{2}}\cdot \dfrac{b}{2A}-\dfrac{1}{1+\left( \dfrac{b^{2}-bx}{2A}\right) ^{2}}\cdot \dfrac{b}{2A}\end{aligned}$$

let $\dfrac{d\left( \alpha +\beta \right) }{dx}$等于zero，得到：

$$\begin{aligned}\dfrac{1}{1+\left( \dfrac{bx}{2A}\right) ^{2}}\cdot \dfrac{b}{2A}&=\dfrac{1}{1+\left( \dfrac{b^{2}-bx}{2A}\right) ^{2}}\cdot \dfrac{b}{2A}\ \\
bx&=b\left( b-x\right) \ \\
x&=b-x\ \\
x&=\dfrac{b}{2}\end{aligned}$$

由此可见，$\alpha +\beta$最大时，该三角形为等腰三角形。接下去，求解此时$\alpha +\beta$的具体数值：

$$\begin{aligned}\tan \alpha &=\dfrac{\dfrac{b}{2}}{\dfrac{2A}{b}}=\dfrac{b^{2}}{4A}\ \\
\alpha &=\tan ^{-1}\dfrac{b^{2}}{4A}\ \\
\alpha +\beta &=2\tan ^{-1}\dfrac{b^{2}}{4A}\end{aligned}$$

有人或许会说没有考虑上顶点向左右延伸至两个下顶点垂直投影以外的情形，是的，我在这里偷懒了，没有做严谨的证明，但是根据草图，会发现向左右延伸得越远，上顶角会逐渐变小，但这只是直观上的结论，要想严谨的证明需要等我心情好一点的时候，还有原题说的是use geometry alone来证明本题，我也是没办法做到，跟心情好坏无关，跟智商有关。