这是一题带星号的附加问题，好在题目本身便给出了解题思路，不过这个解题思路应该是比较常规，没有什么巧妙成分，所以我想作者给这题加星号的原因，或许在于其计算量，但是，计算量好像也不大。废话结束，进入正题。对了，今年大年初三，祝大家新年快乐。

先看原题：

还是老惯例，先画出草图：

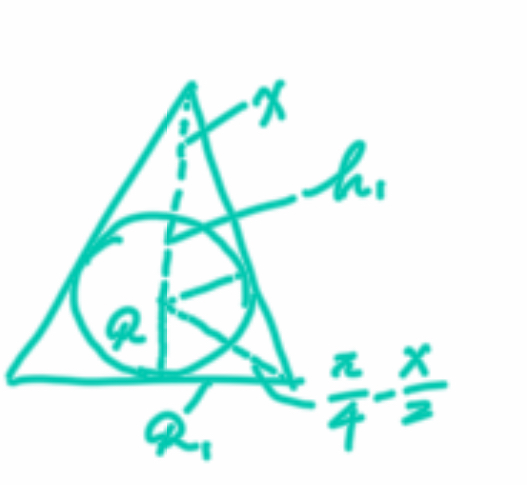
原谅这草图确实很“草”，因为最近作者心情不佳，思绪也并不集中，只能这样了，还是简单说明一下，这是题目所指情形的截面视图。

内部球的半径为：$R$

外部圆锥体的底面半径为：$R_{1}$

外部圆锥体的高为：$H=h_{1}+R$

顶角的一半为：$x$

显然，内部球体的体积为$V_{s}=\dfrac{4}{3}\pi R^{3}$

接下来，我们先写出外部圆锥体的体积表达式（网易云今天的日推也太难听了，shit），圆锥体体积公式为：$V_{c}=\dfrac{1}{3}SH$

先$S$:

由于顶角的一半为$x$，相应底角的一半则为：$\dfrac{\pi }{4}-\dfrac{x}{2}$.

$$\begin{aligned}\dfrac{R}{R_{1}}&=\tan \left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) \ \\
R_{1}&=R\cdot \cot \left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) \end{aligned}$$

所以

$$\begin{aligned}S&=\pi R_{1}^{2}\ \\
&=\pi \cot ^{2}\left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) R^{2}\end{aligned}$$

再来看$H$

$$\begin{aligned}\dfrac{R}{h_{1}}&=\sin x\ \\
h_{1}&=R\cdot \csc x\ \\
H&=h_{1}+R\ \\
&=R\left( 1+\csc x\right) \end{aligned}$$

到此为止，我们得到外部圆锥体的体积表达式：

$$\begin{aligned}V_{c}&=\dfrac{1}{3}SH\ \\
&=\dfrac{1}{3}\pi R^{3}\cot ^{2}\left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) \left( 1+\csc x\right) \end{aligned}$$

接下来，显然只需要对上述表达式进行微分即可。

$$\begin{aligned}\dfrac{dV_{c}}{dx}=\dfrac{1}{3}\pi R^{3}[ \cot \left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) \csc ^{2}\left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) \left( 1+\csc x\right) \
-\cot ^{2}\left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) \csc x\cdot \cot x] \end{aligned}$$

显然，当外部圆锥体体积最小时，上述等式的值为zero。

$$\begin{aligned}\cot \left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) \csc ^{2}\left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) \left( 1+\csc x\right) \
&=\cot ^{2}\left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) \csc x\cdot \cot x\ \\
\csc ^{2}\left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) \left( 1+\csc x\right) &=\cot \left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) \
\csc x\cdot \cot x\ \\
\dfrac{1}{\sin \left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) }\left( 1+\csc x\right) &=\cos \left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) \csc x\cdot \cot x\end{aligned}$$

又因为：

$$\begin{aligned}\sin \left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) &=\dfrac{\sqrt{2}}{2}\left( \cos \dfrac{x}{2}-\sin \dfrac{x}{2}\right) \ \\
\cos \left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) &=\dfrac{\sqrt{2}}{2}\left( \cos \dfrac{x}{2}+\sin \dfrac{x}{2}\right) \end{aligned}$$

所以前一个公式变为：

$$\begin{aligned}\dfrac{1+\csc x}{ \dfrac{\sqrt{2}}{2}c\cos \dfrac{x}{2}-\sin \dfrac{x}{2}) }&=\dfrac{\sqrt{2}}{2}\left( \cos \dfrac{x}{2}+\sin \dfrac{x}{2}\right) \csc x\cot x\ \\
1+\csc x&=\dfrac{1}{2}\left( \cos ^{2}\dfrac{x}{2}-\sin ^{2}\dfrac{x}{2}\right) \csc x\cot x\ \\
&=\dfrac{1}{2}\cos x\csc x\cot x\end{aligned}$$

接下来将等式左右两边均用$\sin x$进行表示，从而计算出$\sin x$

$$\begin{aligned}1+\dfrac{1}{\sin x}&=\dfrac{1}{2}\cos x\cdot \dfrac{1}{\sin x}\dfrac{\cos x}{\sin x}\ \\
\dfrac{\sin x+1}{\sin x}&=\dfrac{\cos ^{2}x}{2\sin ^{2}x}\ \\
\dfrac{2\sin ^{2}x+2\sin x}{2\sin ^{2}x}&=\dfrac{\cos ^{2}x}{2\sin ^{2}x}\ \\
2\sin ^{2}x+2\sin x&=1-\sin ^{2}x\ \\
3\sin ^{2}x+2\sin x-1&=0\end{aligned}$$

let $\sin x=u$

get $$\begin{aligned}3u^{2}+2u-1&=0\ \\
\left( 3u-1\right) \left( u+1\right) &=0\ \\
u&=\dfrac{1}{3}=\sin x\end{aligned}$$

此时，我们发现$V_{c}$的最后部分$\left( 1+cscx\right)$的值为：$$\begin{aligned}1+\csc x&=1+\dfrac{1}{\sin x}\ \\
&=1+3\ \\
&=4\end{aligned}$$

最后一步，当然就是求$\cot ^{2}\left( \dfrac{\pi }{4}-\dfrac{x}{2}\right)$，很简单，对吧？让我们继续吧

$$\begin{aligned}\cot ^{2}\left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) &=\dfrac{\cos ^{2}\left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) }{\sin ^{2}\left( \dfrac{\pi }{4}-\dfrac{x}{2}\right) }\ \\
&=\dfrac{\left[ \dfrac{\sqrt{2}}{2}\left( \cos \dfrac{x}{2}+\sin \dfrac{x}{2}\right) \right] ^{2}}{\left[ \dfrac{\sqrt{2}}{2}\left( \cos \dfrac{x}{2}-\sin \dfrac{x}{2}\right) \right] ^{2}}\ \\
&=\dfrac{1+2\sin \dfrac{x}{2}\cos \dfrac{x}{2}}{1-2\sin \dfrac{x}{2}\cos \dfrac{x}{2}}=\dfrac{1+\sin x}{1-\sin x}\end{aligned}$$

因为$\sin x=\dfrac{1}{3}$,so$$\dfrac{1+\sin x}{1-\sin x}=2$$

最后，我们得到$$\begin{aligned}V_{c}=\dfrac{1}{3}\pi R^{3}\cdot 2\cdot 4=\dfrac{8}{3}\pi R^{3}\
=2V_{s}\end{aligned}$$

证毕！

No time like the present

Παρακαλώ πιστέψτε με για τελευταία φορά