这是定积分原理推导最后一题，其实这题和第二题非常相似，本不打算放在这里再证明一次，但为了完整性，还是这么做了，在你想做一件事的时候，有很多理由支持你去做，也有很多理由想让你放弃这么做，这就是犹豫，但最终总有一方会胜出，只不过是时间问题，但是在时间面前，任何人都需要妥协。

还是先看原题吧

Show that$$\int _{1}^{b}\dfrac{1}{\sqrt{x}}dx=2\left( \sqrt{b}-1\right)$$by using equal subintervals and taking$$x_{k}^{\ast }=\dfrac{x_{k-1}+x_{k}+\sqrt{2x_{k-1}x_{k}}}{4}=\left( \dfrac{\sqrt{x_{k-1}}+\sqrt{x_{k}}}{2}\right) ^{2}$$in formula (12) of Section 6.4.

突然发现上一题的草图同样适用于这一题

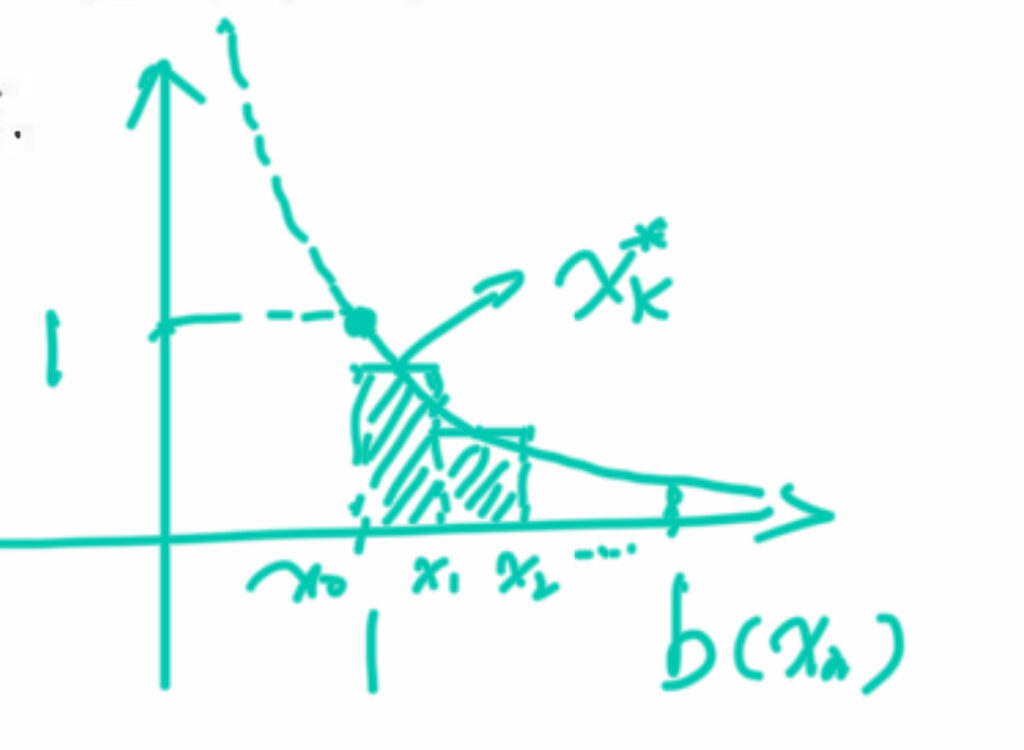
依然是将曲线与X轴之间形成的面积分为n个无限细的长方形，因此每个长方形的底边就是 $\dfrac{b-1}{n}$，为了方便，我们将此记为：$$\Delta x_{k}=\dfrac{b-1}{n}=m$$

从而得到草图中每个长方形底边端点的横坐标为：$$\begin{aligned}x_{0}&=1\ \\
x_{1}&=1+m\ \\
x_{2}&=1+2m\ \\
\vdots \ \\
x_{n}&=1+nm\end{aligned}$$

又因为$$f\left( x\right) =\dfrac{1}{\sqrt{x}}$$

以及前面题目关于 $x_{k}^{\ast }$ 的要求，可以得到每个长方形的高为：

$$\begin{aligned}x_{1}^{\ast }&=\dfrac{1}{ \sqrt{( \dfrac{\sqrt{1}+\sqrt{1+m}}{2}}) ^{2}}=\dfrac{2}{\sqrt{1}+\sqrt{1+m}}\ \\
x_{2}^{\ast }&=\dfrac{1}{\sqrt{\left( \dfrac{\sqrt{1+m}+\sqrt{1+2m}}{2}\right) ^{2}}}=\dfrac{2}{\sqrt{1+m}+\sqrt{1+2n}}\ \\
\vdots \ \\
x_{n}^{\ast }&=\dfrac{1}{\sqrt{\left( \dfrac{\sqrt{1+\left( n-1\right) m}+\sqrt{1+nm}}{2}\right) ^{2}}}=\dfrac{2}{\sqrt{1+(n-1)m}+\sqrt{1+nm}}\end{aligned}$$

从而得到每个长方形的面积为：$$\begin{aligned}S_{1}&=\dfrac{2}{\sqrt{1}+\sqrt{1+m}}\cdot m\ \\
S_{2}&=\dfrac{2}{\sqrt{1+m}+\sqrt{1+2m}}.m\ \\
\vdots \ \\
S_{n}&=\dfrac{2}{\sqrt{1+\left( n-1\right) m}+\sqrt{1+nm}}\cdot m\end{aligned}$$

计算出上述所有长方形面积之和为：$$\begin{aligned}S_{sum}&=\left( \dfrac{2}{\sqrt{1}+\sqrt{1+m}}+\dfrac{2}{\sqrt{1+m}+\sqrt{1+2m}}+ \dots +\dfrac{2}{\sqrt{1+(n-1)m}+\sqrt{1+nm}}\right) m\ \\
&=\left( \dfrac{1}{\sqrt{1}+\sqrt{1+m}}+\dfrac{1}{\sqrt{1+m}+\sqrt{1+2m}}+ \dots +\dfrac{1}{\sqrt{1+(n-1)m}+\sqrt{1+nm}}\right) 2m\end{aligned}$$此处，稍加计算，便可知：$$\begin{aligned}\dfrac{1}{\sqrt{1}+\sqrt{1+m}}&=\dfrac{1\cdot \left( \sqrt{1} -\sqrt{1+m}\right) }{1-1-m}=\dfrac{\sqrt{1} -\sqrt{1+m}}{-m}\ \\
\dfrac{1}{\sqrt{1+m}+\sqrt{1+2m}}&=\dfrac{1\cdot \left( \sqrt{1+m}-\sqrt{1+2m}\right) }{1+m-1-2m}=\dfrac{\sqrt{1+m}-\sqrt{1+2m}}{-m}\ \\
\vdots \ \\
\dfrac{1}{\sqrt{1+\left( n-1\right) m}+\sqrt{1+nm}}&=\dfrac{1\cdot \left( \sqrt{1+\left( n-1\right) m}-\sqrt{1+nm}\right) }{1+\left( n-1\right) m-1-nm}=\dfrac{\sqrt{1+(n-1)m}-\sqrt{1+nm}}{-m}\end{aligned}$$

最后通过几步简单计算和代入，完成最终的证明：

$$\begin{aligned}S_{sum}&=2m\cdot \dfrac{1-\sqrt{1+nm}}{-m}\ \\
&=2\left( \sqrt{1+nm}-1\right) \ \\
&=2\left( \sqrt{1+\dfrac{b-1}{n}\cdot n}-1\right) \ \\
&=2\left( \sqrt{b}-1\right) \end{aligned}$$

HINT:公式若有笔误，还请见谅