在读这本微积分教材时,总会遇到在网上检索不到参考答案的问题,而且美国的教材,书本后面的参考答案不包含推理说明类的题目,大概编者想给学习者一个思考的空间,只要学习者能够通过自己的方式进行推理,且符合逻辑即可。现记录的三题(本文介绍第一题),都是对于定积分原理的推导应用,其实用到的原理都相同,只是形式有些许区别。作此记录的原因有二:1、巩固;2、提醒自己不再犯类似错误(具体错误随文说明)。
1、Show that $\int _{0}^{b}\sqrt{x}dx=\dfrac{2}{3}b^{3/2}$ by taking $x_{k}=\dfrac{k^{2}\cdot b}{n^{2}}$ and $x_{k}^{\ast }=x_{k}$ in formula(12) of Section 6.4.Notice that this problem illustrates the calculation of an integral as a limit by using subintervals of different lengths.
首先,直接用定积分计算公式计算一下,以便和后面用定积分原理计算的答案能够互相对应。
$$\begin{aligned}\int _{0}^{b}\sqrt{x}dx&=\int _{0}^{b}x^{\dfrac{1}{2}}dx\ \\
&=\dfrac{2}{3}x^{\dfrac{3}{2}}] _{0}^{b}\ \\ &=\dfrac{2}{3}b^{\dfrac{3}{2}}-0\ \\ &=\dfrac{2}{3}b^{\dfrac{3}{2}}\end{aligned}$$
再用题目要求的定积分原理来计算,因$y=\sqrt{x}$是一条过原点的曲线,所以这个定积分就是求以下阴影的面积。
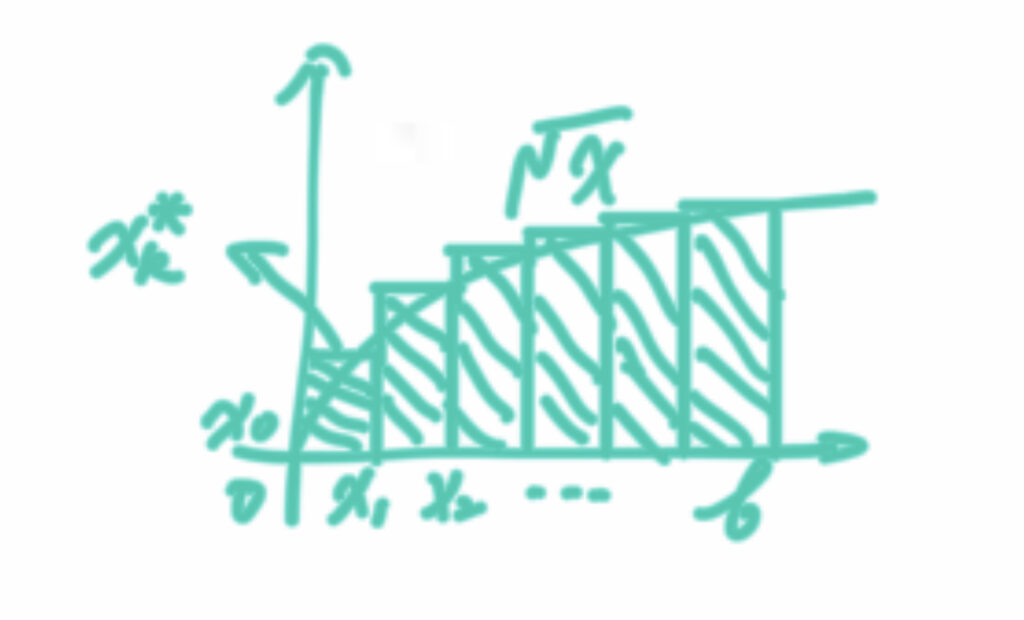
这里我们采用曲线的上端作为每个小长方形的高(采用曲线的下端,会得到相同的结果,在此不做推导),然后题目中提到的formula(12) of Section 6.4为:$$\int _{a}^{b}f\left( x\right) dx=\lim _{\max \Delta x_{k}\rightarrow 0}\sum ^{n}_{x=1}f\left( x_{k}^{\ast }\right) \Delta x_{k}$$
此即为定积分的定义式。
这题对于$x_{k}$有特殊要求的目的在于,想证明前述定积分定义式中$\Delta x_{k}$的值相等或者不相等,均不会影响定积分的计算。
根据 $x_{k}=\dfrac{k^{2}\cdot b}{n^{2}}$
有$$\begin{aligned}x_{1}&=\dfrac{1}{n^{2}}\cdot b\ \\
x_{2}&=\dfrac{4}{n^{2}}\cdot b\ \\
\ \vdots \ \\
x_{n}&=\dfrac{n^{2}}{n^{2}}\cdot b\end{aligned}$$
又根据$f\left( x\right) =\sqrt{x}$,有:
$$\begin{aligned}f\left( x_{1}\right) &=\sqrt{\dfrac{1}{n^{2}}\cdot b}=\dfrac{1\sqrt{b}}{n}\ \\
f\left( x_{2}\right) &=\sqrt{\dfrac{4}{n^{2}}\cdot b}=\dfrac{2\sqrt{b}}{n}\ \\ \ \vdots \ \\
f\left( x_{n}\right) &=\sqrt{\dfrac{n^{2}}{n^{2}}\cdot b}=\dfrac{n\sqrt{b}}{n}\end{aligned}$$
我们将所有长方形的面积之和用$S_{n}$表示,显然,其可由下列公式计算得到:
$$\begin{aligned}S_{n}&=\dfrac{\sqrt{b}}{n}\cdot \dfrac{b}{n^{2}}+\dfrac{2\sqrt{b}}{n}\cdot \dfrac{3b}{n^{2}}\
+\dfrac{3\sqrt{b}}{n}\cdot \dfrac{5b}{n^{2}}+\ldots +\dfrac{n\sqrt{b}}{n}\cdot \dfrac{n^{2}-\left( n-1\right) ^{2}}{n^{2}}\ \\&=\dfrac{b^{3/2}}{n^{3}}+\dfrac{6b^{3/2}}{n^{3}}+\dfrac{15b^{3/2}}{n^{3}}+\ldots +\dfrac{n[n^{2}-\left( n-1\right) ^{2}] b^{3/2}}{n^{3}}\ \\&=\dfrac{b^{3/2}\left[ 1+6+15+\ldots +n\left( 2n-1\right) \right] }{n^{3}}\end{aligned}
接下来就是求解$1+6+15+\ldots +n\left( 2n-1\right)$,写成如下形式:
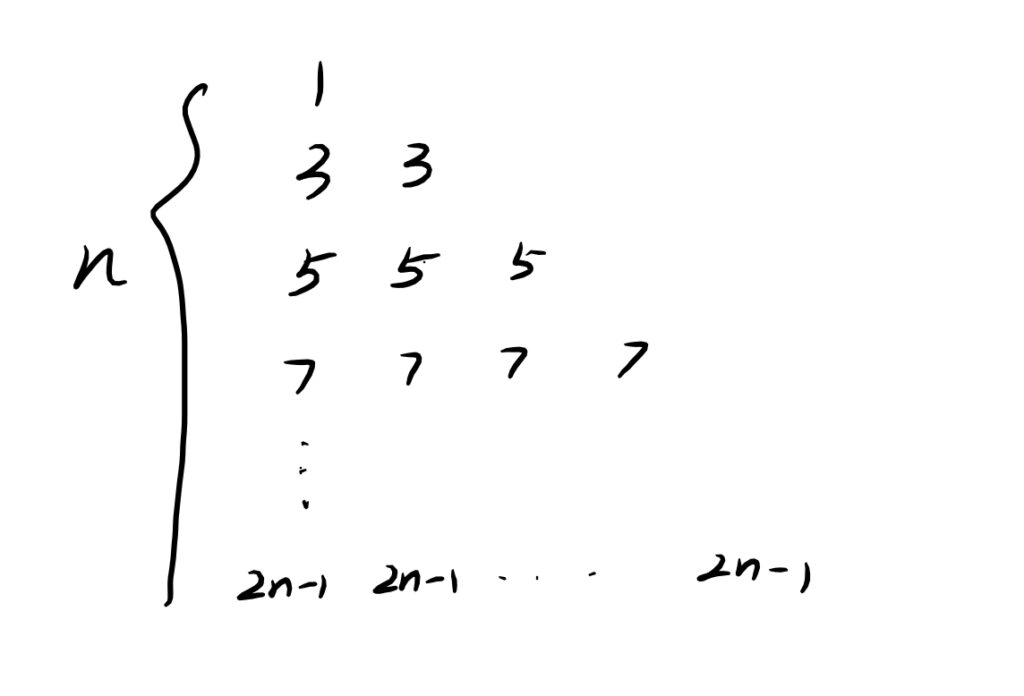
显然,这是一个$n^{\ast }n$的数列,先看第一列的和:$$1+3+5+\ldots +\left( 2n-1\right) =n^{2}$$第二列为$n^{2}-1$,第三列为$n^{2}-4$,第四列为$n^{2}-9$,以此类推,最后一列显然为$n^{2}-\left( n-1\right) ^{2}$。
因此,可以计算出:
$$\begin{aligned}1+6+15+\ldots +n\left( 2n-1\right) \ &=n^{2}+\left( n^{2}-1\right) +\left( n^{2}-4\right) +\ldots +\left[ n^{2}-\left( n-1\right) ^{2}\right] \ \\
&=n^{2}\cdot n-\left[ 1+4+9+\ldots +\left( n-1\right) ^{2}\right] \ \\&=n^{3}-\dfrac{\left( n-1\right) n\left( 2n-1\right) }{6}\end{aligned}$$
到此为止,可以计算出所有长方形的面积之和为:
$$\begin{aligned}S_{n}&=\dfrac{b^{3/2}\cdot \left[ n^{3}-\dfrac{\left( n-1\right) n\left( 2n-1\right) }{6}\right] }{n^{3}}\ \\
&=b^{3/2}\left[ 1-\dfrac{\left( n-1\right) n\left( 2n-1\right) }{6n^{3}}\right] \ \\
&=b^{3/2}\left[ 1-\dfrac{1}{6}\cdot \dfrac{n-1}{n}\cdot \dfrac{n}{n}\cdot \dfrac{2n-1}{n}\right] \ \\
&=b^{3/2}\left[ 1-\dfrac{1}{6}\left( 1-\dfrac{1}{n}\right) \cdot 1\cdot \left( 2-\dfrac{1}{n}\right) \right] \end{aligned}$$
根据定积分的定义,可知$n\rightarrow +\infty $,从而上式中的$\dfrac{1}{n}\rightarrow 0$,从而得到最终的定积分:
$$\begin{aligned}\int _{0}^{b}\sqrt{x}dx&=b^{3/2}\left( 1-\dfrac{1}{6}\times 2\right) \ \\
&=\dfrac{2}{3}b^{3/2}\end{aligned}$$
最终得到验证,与最开始的计算结果相一致。