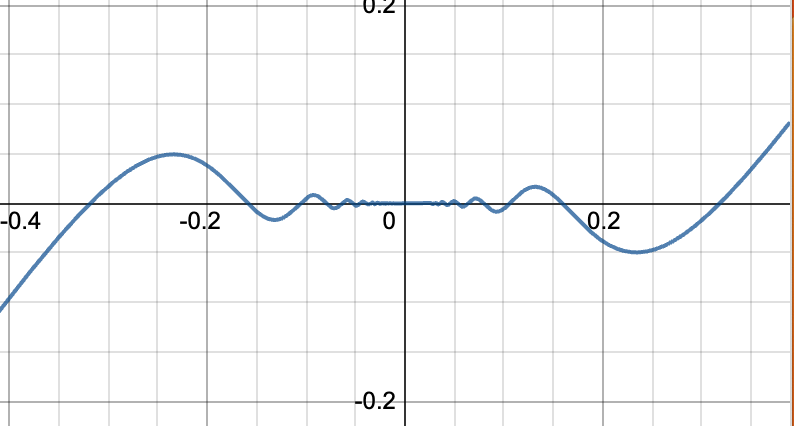
考虑下列问题：

(a) 当x很大时，y会发生什么变化？

(b) 证明f(x)在x=0处是连续的。

(c) 求出x不等于0时的f'(x)。

(d) 找到f'(0)。

(e) 证明f'(x)在x=0处不连续。

(a) 当x很大时，$f(x)$的值会趋近于无穷大或负无穷大，因为$x^{2}$增长的速度比$\sin\dfrac{1}{x}$的振幅变化的速度更快，所以$f(x)$的值会受到$x^{2}$的影响。

(b) 要证明$f(x)$在$x=0$处连续，需要证明当$x$趋近于0时，$f(x)$趋近于$f(0)$。当$x$趋近于0时，$x^{2}\cdot \sin \dfrac{1}{x}$的值会趋近于0，因为$\left\vert x^{2}\cdot \sin \dfrac{1}{x}\right\vert \leq \left\vert x^{2}\right\vert$。因此，当$x$趋近于0时，$f(x)$趋近于$f(0)=0$。因此，$f(x)$在$x=0$处连续。

具体来说，可以使用$\epsilon$-$\delta$的方法来证明$f(x)$在$x=0$处连续：

对于任意给定的$\epsilon>0$，我们需要找到一个$\delta>0$，使得当$0<|x-0|<\delta$时，$|f(x)-f(0)|<\epsilon$。

当$x$不等于0时，$f(x)=x^{2}\cdot \sin \dfrac{1}{x}$。因此，$|f(x)|\leq |x^{2}|$，对于所有的$x$都成立。又因为$x^{2}\to 0$，当$x\to 0$时，所以我们可以选择$\delta=\sqrt{\epsilon}$。这样，当$0<|x-0|<\delta$时，有：$$\left| f\left( x\right) -f\left( 0\right) \right| =\left| x^{2}\cdot \sin \dfrac{1}{x}-0\right| \leq \left| x^{2}\right| <\epsilon$$因此，根据$\epsilon$-$\delta$的定义，$f(x)$在$x=0$处连续。

(c) 当$x$不等于0时，$f(x)$可表示为$f(x)=x^{2}\cdot \sin \dfrac{1}{x}$。使用乘积法则和链式法则，可以求得$f'(x)$为：

$f'(x)=2x\sin\dfrac{1}{x}-\cos\dfrac{1}{x}$

(d) 要找到$f'(0)$，需要求出$f'(x)$在$x=0$处的极限。将$f'(x)$代入上式，得到：

$\lim_{x\to0}f'(x)=\lim_{x\to0}\left(2x\sin\dfrac{1}{x}-\cos\dfrac{1}{x}\right)$

由于$\left\vert2x\sin\dfrac{1}{x}\right\vert\leq\left\vert2x\right\vert$和$\left\vert\cos\dfrac{1}{x}\right\vert\leq1$，因此当$x$趋近于0时，$2x\sin\dfrac{1}{x}$和$\cos\dfrac{1}{x}$都趋近于0。因此，$\lim_{x\to0}f'(x)=0$，即$f'(0)=0$。

hint：为何当$x$趋近于0时，$\cos\dfrac{1}{x}$趋近于0？

这个问题可以从数学上解释。当$x$趋近于0时，$\frac{1}{x}$的绝对值会越来越大，所以$\cos\frac{1}{x}$在单位圆上的振荡频率也会越来越高。具体来说，对于任意的正整数$n$，我们有：

当n是奇数时：$\cos n\pi =-1$

当n是偶数时：$\cos n\pi =1$

因此，当$\frac{1}{x}$趋近于无穷大时，$\cos\frac{1}{x}$在单位圆上的振荡次数会越来越多，同时振荡幅度也会越来越大。这就是为什么$\cos\frac{1}{x}$在$x$趋近于0时会发生快速的周期性振荡。

另一方面，$\frac{1}{x}$在$x$趋近于0时的增长速度是非常快的，因为$\frac{1}{x}$在$x$趋近于0时的导数是无穷大。因此，$\frac{1}{x}$的增长速度会比$\cos\frac{1}{x}$更快，从而可以将$\cos\frac{1}{x}$在$x$趋近于0时近似看作0，并得到$f'(0)=0$的结果。

(e) 为了证明$f'(x)$在$x=0$处不连续，需要证明$\lim_{x\to0}f'(x)$不存在。考虑两个不同的极限路径：$x_{n}=\dfrac{1}{n\pi}$和$y_{n}=\dfrac{1}{n\pi+\frac{\pi}{2}}$。当$n$趋近于无穷大时，$x_{n}$和$y_{n}$都趋近于0。然而，当$n$趋近于无穷大时，$f'(x_{n})$的绝对值趋近于1，而$f'(y_{n})$的绝对值趋近于0。因此，$\lim_{x\to0}f'(x)$不存在，即$f'(x)$在$x=0$处不连续。