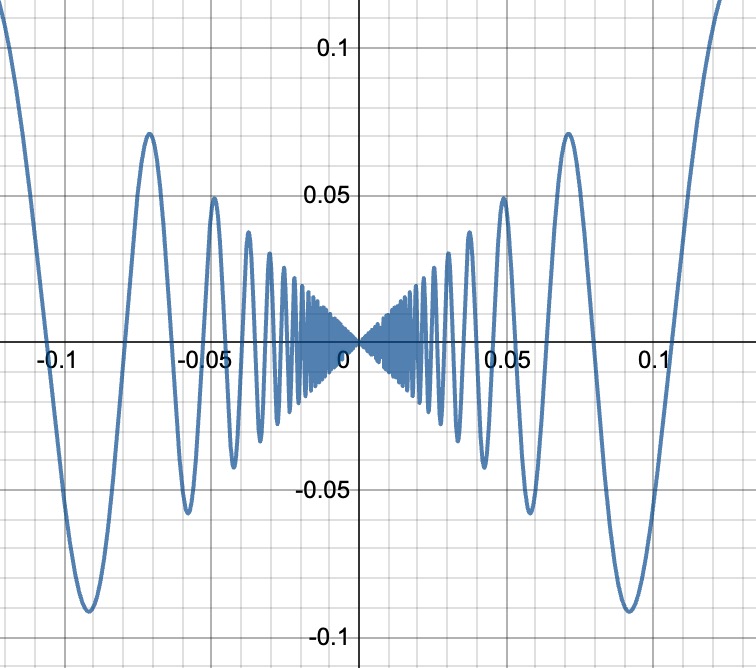
要证明这个函数在x=0时是连续的，我们需要证明$\lim\limits_{x\rightarrow 0} f(x) = f(0)$，其中$f(x)$是该函数。

首先考虑当$x\neq 0$时，$f(x) = x\cdot\sin\dfrac{1}{x}$是连续的，因为$x$和$\sin\dfrac{1}{x}$都是连续的函数。因此，我们只需要证明$\lim\limits_{x\rightarrow 0} f(x) = 0$。

对于任意$\epsilon > 0$，我们需要找到一个$\delta > 0$，使得当$0<|x|<\delta$时，$|f(x)|<\epsilon$。由于$|\sin x|\leq 1$，我们有：

$$|f(x)| = |x\cdot \sin \frac{1}{x}| \leq |x|$$

因此，我们可以选择$\delta=\epsilon$。当$0<|x-0|<\delta$时，我们有：

$$|f(x) - f(0)| = |f(x)| \leq |x| < \delta = \epsilon$$

这说明在x=0时，该函数是连续的。

接下来，我们需要证明该函数在x=0处的导数不存在。我们可以使用函数的定义来计算导数：

$$f'(0) = \lim\limits_{x\rightarrow 0} \frac{f(x)-f(0)}{x-0} = \lim\limits_{x\rightarrow 0} \frac{x\cdot\sin\dfrac{1}{x}}{x} = \lim\limits_{x\rightarrow 0} \sin\dfrac{1}{x}$$

由于$\sin\dfrac{1}{x}$在$x\rightarrow 0$时没有极限，因此$f'(0)$不存在，即该函数在x=0处的导数不存在。

关于$\sin\dfrac{1}{x}$在$x\rightarrow 0$时为何没有极限的问题：

当 $x$ 趋近于 $0$ 时，$\sin \frac{1}{x}$ 的值会在 $[-1,1]$ 之间震荡。因为 $\frac{1}{x}$ 可以取到非常大的值，使得 $\sin \frac{1}{x}$ 的振幅也会变得非常大。具体来说，对于任何给定的正数 $M$，可以找到两个数 $x_1$ 和 $x_2$，满足 $0 < |x_1| < |x_2| < \frac{1}{\pi M}$，使得 $\sin \frac{1}{x_1} = -1$，$\sin \frac{1}{x_2} = 1$。因此，当 $x$ 趋近于 $0$ 时，$\sin \frac{1}{x}$ 没有极限。

这个结论也可以通过反证法来证明。假设 $\lim_{x \to 0} \sin \frac{1}{x}$ 存在，设其极限为 $L$。则对于任意 $\epsilon > 0$，存在 $\delta > 0$，使得当 $0 < |x| < \delta$ 时，$|\sin \frac{1}{x} - L| < \epsilon$。选择 $\epsilon = 1$，则存在 $0 < |x_1| < |x_2| < \delta$，使得 $\sin \frac{1}{x_1} = -1$，$\sin \frac{1}{x_2} = 1$。因此，$|-1 - L| < 1$ 和 $|1 - L| < 1$，推出 $L \leq -2$ 和 $L \geq 2$，与 $|\sin \frac{1}{x}| \leq 1$ 矛盾。因此，假设不成立，$\sin \frac{1}{x}$ 在 $x \to 0$ 时没有极限。

关于第一个问题，即证明这个函数在x=0时是连续的，为何不能采用证明左右极限相等的方法来证明？

首先，我们计算左极限：

$$\lim_{x\to 0^-} f(x) = \lim_{x\to 0^-} x\cdot\sin\dfrac{1}{x}$$

当$x\to 0^-$时，$\dfrac{1}{x}\to -\infty$，因此$\sin\dfrac{1}{x}$在$x\to 0^-$时振荡无限，没有极限。因此，左极限不存在。

接下来，我们计算右极限：

$$\lim_{x\to 0^+} f(x) = \lim_{x\to 0^+} x\cdot\sin\dfrac{1}{x}$$

当$x\to 0^+$时，$\dfrac{1}{x}\to +\infty$，因此$\sin\dfrac{1}{x}$在$x\to 0^+$时也振荡无限，没有极限。因此，右极限也不存在。

由于左右极限都不存在，所以该函数在$x=0$处不连续。

因此，我们不能使用左右极限相等的方法来证明该函数在$x=0$时是连续的。